A search algorithm is admissible if it is guaranteed to find a minimal path to a solution whenever such a solution exists. Breadth first search is admissible, because it looks at every state at level n before considering any state at level n+1.
Let's characterize a class of admissible heuristic search strategies,
using the evaluation function:
f(n) = g(n) + h(n)
As we saw in previous notes, g(n) represents the actual distance at which the state n has been found in the graph, and h(n) is the heuristic estimate of the distance from n to a goal state. So f(n) represents an estimate of the total cost of the path from the start, through n to the goal.
Let's define the evaluation function f*:
f*(n) = g*(n) + h*(n)
where g*(n) is the cost of the shortest path from the start to n and h*(n) returns the actual cost of the shortest path from n to the goal. So f* is the actual cost of the optimal path from the start to the goal through n.
We call the function f* an oracle -- an ideal evaluation function that can see the shortest path from the start to the goal. Of course, oracles of this type don't exist for most search problems. For real problems, we want an evaluation function, f, that approaches f*
Algorithm A: In algorithm A, g(n), the cost of the
current path from start to n, is a reasonable estimate of g*:
g(n) >= g*(n)
g(n) and g*(n) will only be equal if the search has found the optimal path to n. Similarly, in algorithm A, we replace h*(n) with h(n). Although we can't actually compute h*(n), we can often determine whether h(n) is bounded by h*(n) -- that is, we can often determine that h(n) is less than or equal to the actual cost of a minimal path (h*(n)).
Algorithm A: Algorithm A is the best-first search algorithm plus the evaluation function f(n) = g(n) + h(n).
Algorithm A*: is algorithm A in which
h(n) <= h*(n)
for all states n. In other words, if an algorithm uses an evaluation function that underestimates the cost to the goal it is an A* algorithm.
Key Point: All A* algorithms are admissible.
Breadth-first Search is an A* algorithm in which
f(n) = g(n) + 0
In other words, bread-first search uses a trivial estimate of the distance to the goal.
Route Finding Example: For route-finding problems, the straight-line distance from city n to a goal city is a lower bound on the distance of an optimal route from n to the goal.
Eight puzzle Example: The heuristic of number of tiles out-of-place is certainly less than the actual number of moves to the goal state. So this heuristic (combined with best-first search) is an admissible algorithm. So is the heuristic sum of the distances of out-of-place tiles, because it too underestimates the actual number of moves required to reach a goal state.
In other words, for any two states in the search space, a monotonic heuristic always underestimates the cost of going from ni to nj. The heuristic is everywhere admissible.
If best-first search is used with a monotonic heuristic, you can skip checking for shortest path when a state is encountered a second time. The second occurrence will not be shorter because the heuristic finds the shortest path to any state the first time the state is found. Thus, for a monotone heuristic, searching a graph is no different from searching a tree.
Any monotonic heuristic is admissible. For some sequence of states, s1, s2, s3,...,sg, from start to goal, if the heuristic underestimates the cost of going from s1 to s2 and from s2 to s3 and so on, then it underestimates the cost of going from any state to the goal. So, it follows that h(n) <= cost(sn, sg) = h*(n).
For two A* heuristics, h1 and h2, if h1(n) <= h2(n), for all states n in the search space, then heuristic h2 is more informed than h1.
Eight Puzzle Heuristics: Breadth-first search is an
A* heuristic with h1(n) = 0, for all n. We have also
noted that h2, the number of tiles out of place is a lower bound
for h*. So it follows that:
h1 <= h2 < h*(n)
Therefore, "number of tiles out of place" is more informed than breadth-first heuristic. This should be obvious.
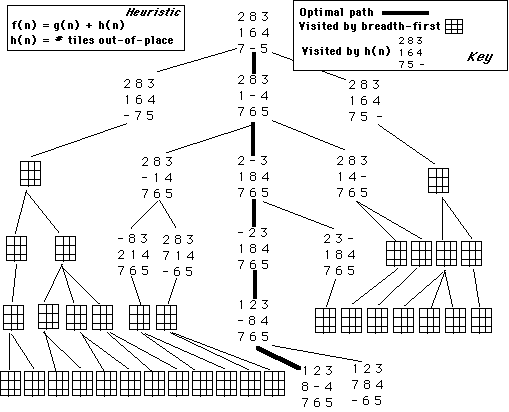
The following figure illustrates the difference between the "number of out-of-place tiles" heuristic and breadth-first search. The heavy dark line shows the optimal solution path. The states that show the numbers on the tiles are the states that would be the portion of the space that is searched by the "tiles out-of-place" heuristic. The rest of the states shown are the ones that would also be examined by breadth-first search. You can see the significant pruning done by the more informed heuristic.
