CS Principles
This activity introduces the concept that abstractions built upon
binary sequences can be used to represent all digital data
. It also introduces the idea the computing has global
impacts. It focuses, in part, on the following learning
objectives:
- 5: The student can describe the combination of abstractions used to represent data.
- 6: The student can explain how binary sequences are used to represent digital data.
- 28: The student can analyze how computing affects communication, interaction, and cognition.
- 29: The student can connect computing with innovations in other fields.
- 30: The student can analyze the beneficial and harmful effects of computing.
- 31: The student can connect computing within economic, social, and cultural contexts.
Bits as the Natural Unit of Information
This was the seminal insight
of Claude
Shannon, founder of information and communication theory. As this
chapter illustrates all information stored on computers (documents,
photos, songs, etc.) and communicated through the Internet (email,
blogs, twitter posts, etc.) are represented as bits, zeros and ones.
Digital data are represented in discrete bits
(Binary digITs). Analog data are represented as
a continuous quantity. Think of the difference between a digital
watch that displays hours, minutes, seconds, and tenths of a
second, and an analog clock, with hour hand, minute hand, and a
sweep second hand.
- Think of the difference in fidelity between
digital
vs. analog recordings.
Moore's Law
- Moore's
law is the observation that the number of transistors that could
be packed onto a integrated circuit seemed to double ever two years or
so. This remarkable trend
about exponential
growth in chip density has proved to be true for 40 years now.
- Someone offers you a summer job and offers you two payment
schemes: (1) $10 per hour for 40 hours per week for 30 days or (2) One
cent on day 1, two cents and day two, four cents on day three and on
(doubling each day) for 30 days. Which play would you
choose? Click
here to see how exponential growth affects this question.
It's All Just Bits
- Binary digits (bits) correspond naturally to electronic
circuits where 1 represents 'on' and 0 represents 'off'. In
computers, binary sequences are used to represent all kinds of data:
text, numbers, images, sounds, ..., everything.
- Depending on the context, the same string of bits can represent
different types of information. These are all examples of abstraction
at work:
- The sequence 0100 0001 can represent the binary numeral for the decimal value 65
when it occurs calculator.
- The sequence 0100 0001 can represent the ASCII letter 'A' when it occurs in an email message.
- The sequence 0100 0001 can represent the amount of Red in the RGB color model
when it occurs in an image.
- The sequence 0100 0001 can represent the MOV B,C machine operation on
the Intel
8080 8-bit processor
A Little Bit About Bits
A byte is an 8-bit sequence. Historially an 8-bit byte was
used to represent a single character in computer memory.
The length of a binary sequence -- a sequence of 0s and 1s --
determines the number of different sequences that can be generated and
therefore the number of different things that can be represented by
such a sequence.
For example, with 1 bit, you can have two different sequences, 0 or 1,
which can stand for two different colors, say, 0 stands for white and 1 for black.
With 2 bits, you can have four different sequences, 00, 01, 10, or 11, which
can represent four different colors, white, black, red, green. And so on.
In general, an n-bit sequence can represent 2n different things.
Here's how:
| Number of bits | Number of things | Representations |
|---|
| 1 | 2 (i.e., 21) | 0, 1 |
| 2 | 4 (i.e., 22) | 00, 01, 10, 11 |
| 3 | 8 (i.e., 23) | 000, 001, 010, 011, 100, 101, 110, 111 |
| 4 | 16 (i.e., 24) | 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 |
| 5 | 32 (i.e., 25) | |
| 6 | 64 (i.e., 26) | |
| 7 | 128 (i.e., 27) | |
| 8 | 256 (i.e., 28) | |
Data Abstraction: How Colors Are Represented in Bits
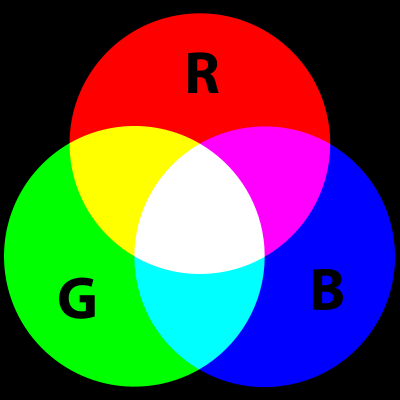
- The RGB
model adds together 3 primary colors, Red, Green, and Blue, where
each color component (R,G,B) is represented as an 8-bit byte.
If there are 256 (28) possible values for each of
R,G,B, the triplet can represent 256 × 256 × 256 =
16,777,216 different colors, which corresponds well to the number of
colors the human eye can distinguish.
(R, G, B)
(65,65,65) = Grey
(255,0,0) = Red
(0,255,0) = Green
(0,0,255) = Blue
(65,0,0) = Brown
Try to mix your own colors: Colorschemer.com
Perfection is Normal
- Because they are based on strings of discrete bits, digital (as opposed
to analog) copies are perfect copies.
- Computer scientists and engineers have developed
effective error
detection and error correction schemes to insure accurate data
representation and communication.
Example: Parity Bit Error Detection
Suppose you are sending a stream of data to a server. By adding
a parity bit, you enable to the server to detect some basic
transmission errors. For example, if the server expects that every
byte will contain an even number of 1s and it detects a byte
such as 0001 0101 with an odd number of 1s,
it can tell that an error occured. Perhaps the user meant to
send 0000 0101 but one of the bits was
flipped from 0 to 1 during transmission.
A parity bit is a bit that is added as the leftmost bit of
a bit string to ensure that the number of bits that are 1 in the bit string
are even or odd.
To see how this works, suppose our data are stored in strings containing 7 bits.
In an even parity scheme the eighth bit, the parity
bit, is set to 1 if the number of 1s in the 7 data bits is odd,
thereby making the number of 1s in the 8-bit byte an even number. It
is set to 0 if the number of 1s in the data is even.
In an odd parity scheme the eighth bit, the parity
bit, is set to 1 if the number of 1s in the 7 data bits is even,
thereby making the number of 1s in the 8-bit byte an odd number. It
is set to 0 if the number of 1s in the data is odd.
The following table summarize this approach.
| Data Bits (7) | Add a parity bit to get 8 bits |
|---|
Even Parity
Total number 1s is even | Odd Parity
Total number of 1s is odd |
|---|
| 000 0000 (0 1s) | 0000 0000 | 1000 0000 |
| 011 0010 (3 1s) | 1011 0010 | 0011 0010 |
| 011 0011 (4 1s) | 0011 0011 | 1011 0011 |
| 011 0111 (5 1s) | 1011 0111 | 0011 0111 |
Question: What would happen in this scheme if 2 bits were switched from 1 to 0 or 0 to 1?
Want in the Midst of Plenty
- Data
storage devices change. Data stored on floppy disks (in my
office) are no longer easily retrievable.
Nothing Goes Away
- Today massive amounts of data (and data about us) are
stored on databases in multiple copies. These data will never go
away. Computer scientists are working hard to
develop data
mining algorithms to retrieve and analzye these data. Think of
the law enforcement and privacy implications.
- Example: NPR Story on Mobile Face Recognition App
Bits Move Faster Than Thought
Discussion: Technology is Neither Good nor Bad?
- Is it true that the digital explosion is "neither good
nor bad" but has both positive and negative implicaitons? Examples?
- Is it true that technology, in general, brings both risks and opportunities?
Examples?
Self-study
The material in this chapter and this lecture will be on Friday's quiz.
See Friday's schedule for some self-study
exercises on this material.


