
 |
CPSC 110-08: Computing on Mobile Phones |
In programming procedural abstraction is the use of procedures to help manage the complexity of programs.
In general, abstraction is the ability to filter out information that is not necessary to a problem and to generalize those details that are significant.
In previous lectures we have seen how to define and use procedures. A procedure is a named module that can be called or invoked at one or more places in the program. A procedure contains an algorithm in its do slot.
We have already used the following block to define procedures that
perform a sequence of actions but do not return a result:
We now want to learn to define and use special types of procedures
that do return results. These are typically called functions.
A function is procedure that takes 0 or more arguments and returns a
value. In App Inventor a function is defined using the following block:
Notice the additional slot labeled return at the bottom of the block.
You are already familiar with built-in functions in App Inventor.
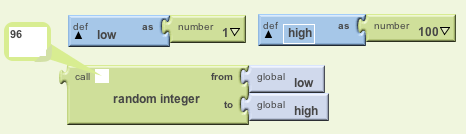
For example, you've been using the random integer function,
which takes two arguments, from and to and returns a random
integer between from and to inclusive:

A function's arguments are place holders into which
you can place values. For example, the following use of the random
integer function will return a random number between 1 and 100:

You can call or invoke a function (or a procedure) in
the blocks editor by right-clicking and using the "Do It" option:

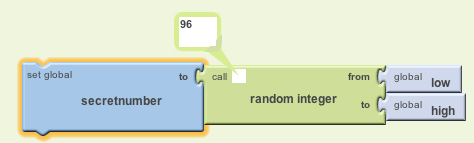
Note that we don't always want to plug literal values, like 100,
into an argument slot. We can also plug in the value of a variable.
Invoking a function produces a value and that value can be
placed inside of any slot that takes a value:
App Inventor gives us the ability to write our own functions using the procedureWithResult
block. Note that it has an open slot for an argument and an open slot for a return value
and a do slot where we can place a sequence of statements:
To see how this works, let's define a trivial function that
calculates the square of any number and then call the
function and pass it the argument 10.
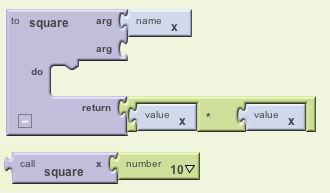
Note that calling our square function looks similar (except for the colors) to calling the random integer function.
In this case the function is so simple that there is nothing to "do" other than perform the calculation and return the result. So we can just put our calculation in the return slot.
Of course, we wouldn't typically define a procedure for such a simple calculation. So let's look at a more likely example.
Our simple square function contains an argument where you plug in the value that you want to square. So, rather than having to define separate functions to calculate specific values -- e.g., squareOf10, squareOf2, squareOfMinus3 -- you define a much more general function, square(X) where any value can be plugged in for X.
Thus, arguments make our functions and procedures more general, giving them wider application. This generality is an important characteristic of procedural abstraction.
Suppose your app needs to calculate the hypotenuse of a right triangle. You probably remember the Pythagorean Theorem from high school geometry -- i.e., the formula for calculating the length of the hypotenuse of a right triangle based on the lengths of its other two sides. The length of the hypotenuse is equal to the square root of the sum of the squares of the other two sides:
c = √ a2+ b2
The Pseudocode algorithm for computing the hypotenuse is quite simple. The only thing we need to do is return the square root of the sum of the squares of a and b:
# Comment: A function to compute the hypotenuse # Notice that we put the parameters, a and b, in a list following the function's name. To hypotenuse(a, b): Return: sqrt(a * a + b * b)
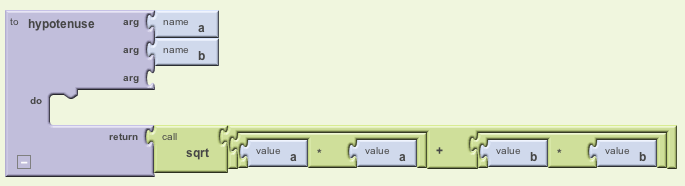
Here again, there is nothing to "do" besides perform the calculation so we just return the result of calculating √ a2+ b2 .
Note that we don't need a global variable to calculate the hypotenuse. We can just return the value of the hypotenuse.
A parameter (or an argument as they are called in App Inventor) is a place holder in a function or procedure definition. When you call the function you substitute a value for the parameter and the function uses that value in its computation.
For example, the hypotenuse(a,b) function has two parameters, a, and b. When I call this function, I would replace a and b with specific values. For example if I call hypotenuse(4, 3), it will compute √ 42+ 32 = 5.
The values that are used as arguments don't have to be literal values like 4 and 3. They can be values contained in variables. For example, suppose that we have set X to the value 5 and Y to the value 12. Then when we call hypotenuse(X,Y), it will compute √ 42+ 32 = 13.
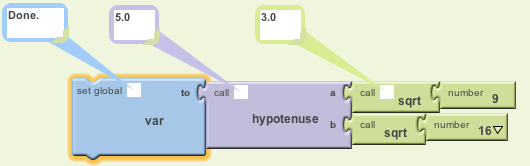
The values that we plug into a parameter can also be the result of a function call. For example, what value would Var be set to by the following algorithm:
Set Var to hypotenuse(sqrt(9), sqrt(16))
Here is how this would look in App Inventor:
Another way of defining our hypotenuse function is to use a global variable, Hypotenuse, and break the computation into several steps storing the intermediate results in Hypotenuse, and then returning Hypotenuse as the function's result:
# Comment: A function to compute the hypotenuse # Notice that we put the parameters, a and b, in a list following the function's name. To hypotenuse(a, b): Set Hypotenuse to a * a Set Hypotenuse to Hypotenuse + (b * b) Set Hypotenuse to sqrt(Hypotenuse) Return: Hypotenuse
Here's a function that will perform this algorithm in App Inventor:
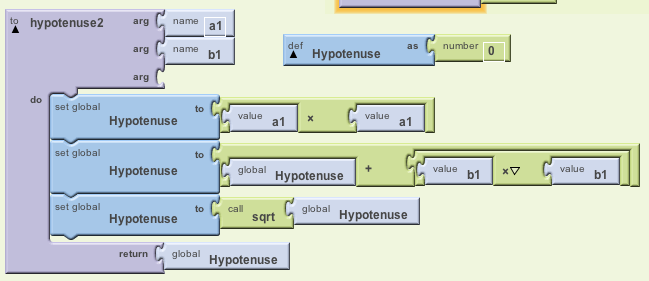
(NOTE: Unlike in most programming languages, in App Inventor, argument names have global scope, rather than local scope, which means we can't reuse the argument names a, and b, in this function definition. So we use a1 and b1.)
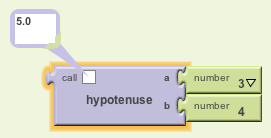
Before you use your function in your app, you should test it by calling it. To do this, you will need to pull out the call function block from the My Definitions drawer.
If you right-click on a call to the function, you can test it using App Inventor's Do-it option, as shown here:
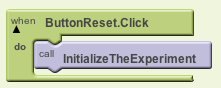
A procedure call is a statement and it can go
anywhere that a statement can go in a program. For example, it can go
in a do slot. Recall this example from the FairCoin app,
where we Call InitializeTheExperiment to do some initialize
operations for us:
A function call produces a value, which cannot stand
alone the way a statement can. Therefore the value has to be put into
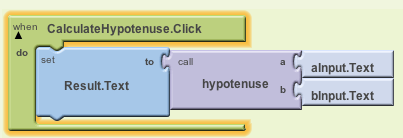
a statement or into another expression. For example, look how we put
the result of calculating the hypotenuse into the slot that takes a
text value.
F = 9⁄5C + 32.
According to this formula 100 degrees Celsius is 212 Fahrenheit (the boiling point of water) and 0 degrees Celsius is 32 degrees Fahrenheit (the freezing point).
This function should take 1 argument, C, that represents the temperature in Celsius. And it should return the equivalent temperature in Fahrenheit. Copy the style of the pseudocode examples given above.
Post your Pseudocode and a picture of your App Inventor function on a Portfolio page.