|
CPSC 110-08: Computing on Mobile Phones
|
This homework is a follow-up to the How to Flip a Coin tutorial, where we learned how to use App Inventor's pseudo random number generator (PRNG) to simulate a coin flip.
Recall that App Inventor's PRNG is a generates a random-looking sequence by means of a deterministic function that computes the n+1st value in the sequence from the nth value:
Xn+1 = (aXn + b) mod m
Thus, a PRNG is model of a truly random process. For any such model, it is natural to ask: ow good is App Inventor's PRNG? How well does it model a truly random process?
One way to test the quality of App Inventor's PRNG is to see how well it does at simulating a random process such as flipping a coin. We all know that if you flip a coin it will come up either heads or tails. But suppose you repeatedly ran an experiment where you flip a real coin 10,000 times and it came up heads an average of 3,938 times and tails an average of 6,062 times, as summarized in the following table:
Trial nTosses nHeads nTails 1 10,000 4000 6000 2 10,000 3985 6015 3 10,000 3995 6005 4 10,000 3700 6300 5 10,000 4010 5990 Averages 10,000 3938 6062
If you received these results, you would doubt whether the coin is truly fair? Maybe it is rigged somehow?
Similarly, if you are using App Inventor's PRNG to model a coin toss, then over the long run it should produce roughly 50% heads and 50% tails.
In this tutorial we design an app that helps us to test how good the PRNG is at simulating random events. We will use a while loop to generate a sequence of coin flips and count the numbers of heads and tails.
Download the source code for Fair Coin Experiment app, save it as a zip file on your computer, and then upload it into App Inventor.
Read the description of the app (below), read the app's source code, and figure out how the app works.
Conduct the following experiment on both your phone and the App Inventor emulator:
Run at least 10,000 trials of the coin-flip experiment on both the phone and the emulator and record the number of total flips, number of heads, and number of tails.NOTE: The app is kind of slow. So rather than running 10,000 trials in a single experiment. Run a smaller number of trials -- e.g., 1000 -- and repeat the experiment.
Not Responding Message: If you get this message, click the "continue" option rather than the quit option -- the app is just slow.
Create a portfolio page for this homework and paste your experiments' results. Then answer and justify your answer to the following question:
Is App Inventor's PRNG, as implemented on the emulator and as implemented on the phone, a good model for a random process such as flipping a coin?
Let's write an app to help us perform this experimental test of App Inventor's PRNG.
Our app must let the user input how many times they want to 'flip' the coin and must report how many heads and tails were obtained. To do this, our user interface will contain the following components:
Component Purpose TextBoxNumFlips Let's the user input the number of times to 'flip' the coin LabelToss Labels the TextBox LabelHeads Reports the number of heads obtained LabelTails Reports the number of tails obtained ButtonStart Flips the coin repeatedly until desired number of flips is obtained ButtonReset Resets all counters so the experiment can be repeated.
The app will use these components to produce the following user
interface (click to enlarge):
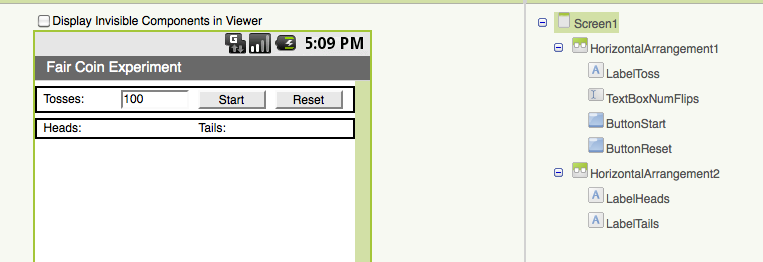
The idea here is that the user can input a number indicating how many Tosses. When the button is clicked, the app will simulate that many coin tosses and record and display the number of heads and tails.
What variables do we need for this app? That depends on what objects we want to model and what data we want to remember. In this app we are modeling a two-sided coin, so we should have a Coin variable. And we need to count how many times it comes up heads and tails. So we need a couple of counter variables. And we need a variable to remember how many times the user wants us to 'flip' the coin. Also, because we will need to repeatedly flip the coin, we will need a variable to keep track of the number of times we have repeated the loop.
Thus, our app defines the following variables:
Variable Purpose Coin Model: Represents a 2-sided coin where 1 represents heads and 2 represents tails nFlips Loop limit: Represents how many times the user wants to flip the coin. nHeads Counter: Counts the number of heads obtained nTails Counter: Counts the number of tails obtained flip Loop counter: counts how many times we have 'flipped' the coin
To make it easier to implement our experiment our app will be divided into procedures that represent the basic steps. This will allow us to think about the experiment at a higher level of abstraction.
We'll need a procedure to initialize the experiment -- i.e., set it up. Another procedure to perform a coin flip and keep track of whether it is heads or tails. And another procedure to report the results. This leads to the following design:
Procedure Purpose InitializeTheExperiment Initialize all the variables and data we use to keep track of the results. ReportTheResults Display the number of heads and tails in the user interface. DoOneCoinFlip Simulate the coin flip and count whether it was a head or a tail.
Let's now develop the algorithms for each of these procedures. The InitializeTheExperiment procedure is just a simple sequence of assignment statements -- i.e., statements that set the values of certain variables:
# Comment: InitializeTheExperiment -- set all the variables to 0 # and initialize the labels to 0 and get the number of flips from # the text box. To InitializeTheExperiment Set nHeads to 0 Set nTails to 0 Set LabelHeads.Text to "Heads: 0" Set LabelTails.Text to "Tails: 0" Set nFlips to TextBoxNumFlips.Text |
 |
#Comment: Set the labels for number of heads and number of tails To ReportTheResults Set LabelHeads.Text to "Heads: " joined-with nHeads Set LabelTails.Text to "Tails: " joined-with nTails |
|
#Comment: Generate a random integer between 1 and 2 inclusive and
# increment the appropriate counter for heads or tails.
To DoOneCoinFlip
Set Coin to a random integer between 1 and 2
If Coin = 1 then-do:
Set nHeads to nHeads + 1
else-do:
Set nTails to nTails + 1
|
|
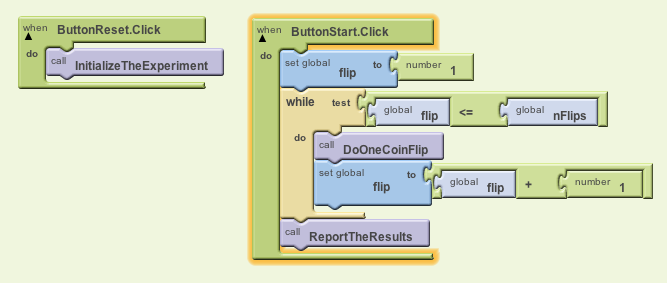
This app has two event handlers, one for each button. The algorithm for the ButtonReset button is very simple. It just needs to call the InitializeTheExperiment procedure that we wrote:
# Comment: When the ButtonReset is clicked, initialize the experiment. When ButtonReset.Click Call InitializeTheExperiment
The algorithm for ButtonStart event requires a loop. When this button is clicked we want to flip the coin nFlips number of times. So we need to initialize our loop counter to 1 and then loop through the steps of flipping the coin and incrementing the counter. When the loop finishes, we should report the results.
# Comment: Repeat the coin flip from 1 to nFlips number of times.
When ButtonStart.Click
Set flip to 1
While flip <= nFlips do:
Call DoOneCoinFlip
Set flip to flip + 1
Call ReportTheResults
Notice how much easier it is to read and understand this algorithm now
that we are hiding some of the details in the procedures. This is also
true for the App Inventor blocks:
