CPSC 352 -- Artificial Intelligence
Notes: Explanation Based Learning (EBL)

Overview of EBL

Explanation based learning (EBL) uses an explicit domain theory to construct an explanation or proof of a training example. By then generalizing from the proof, new knowledge is acquired that can be applied in non-training situations.

This differs from inductive learning in that the domain theory implies the new knowledge. It is sometimes called deductive learning or analytic learning.

Example: Learning When an Object is a Cup

Target Concept: cup(C) :- premise(C).

Domain Theory: 

   cup(X) :- liftable(X),
	     holds_liquid(X).
   holds_liquid(Z) :- part(Z,W),
		      concave(W),
		      points_up(W).
   liftable(X) :- light(X), part(Y,handle).
   light(X) :- small(X).
   light(X) :- made_of(X,feathers).

Note that the domain theory includes the knowledge needed to determine when something is a cup. We want an explicit rule that specifies when something is a cup.

Training Example: An Instance of a Cup 

  cup(obj1)          small(obj1)       part(obj1,handle)
  owns(bob,obj1)                       part(obj1,bottom)
				       part(obj1,bowl)
  points_up(bowl)
  concave(bowl)
  color(obj1,red)

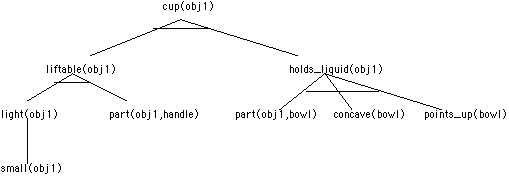
Proof (or Explanation): Use the domain theory to prove that the instance is a cup. Then generalize the proof.

First: Prove that obj1 is a cup.

Next: Generalize the proof to: X is a cup. To generalize, we generalize all constants that depend solely on the training example. So bowl and obj1 are constants found in the training example but not in the domain thoery.

Next: Add the new chunk of knowledge to the domain theory. 

   cup(X) :- small(X), 
             part(X,handle),
             part(X,W),
             concave(W),
             points_up(W).

Note that none of the irrelevant information in the training example has made it into the proof or into the new knowledge.

The new rule can be used to identify a cup.