CPSC 352 -- Artificial Intelligence
Notes: Algorithms & Approaches: Symbolic AI
Introduction
In this and the next lecture we consider three basic approaches to AI, all of which involve
some form of knowledge representation and search:
- Symbolic Representation + Recursive Search
- Neural Networks
- Genetic Algorithms
In this lecture we focus on the symbolic approach. In the next lecture we take up
the other two.
Illustration of Knowledge Representation
Can a chessboard, with its top-left and bottom-right squares removed, be tiled
by a set of dominoes?

Exercise: Is this a search problem? How would you represent
this problem abstractly? How would you solve this problem?.
AI as Knowledge Representation and Search
The study of logic and computers has revealed to us that
intelligence resides in physical symbol systems. This is computer science's
most basic law of qualitative structure. Symbol systems are collections of patterns
and processes, the latter being capable of producing, destroying, and modifying
the former. The most important property of patterns is that they can designate
objects, processes or other patterns, and that when they designate processes they
can be interpreted...
A second law of qualitative structure for artificial intelligence is that
symbol systems solve problems by generating potential solutions and testing them
-- that is by searching. Solutions are usually sought by creating symbolic
expressions and modifying them sequentially until they satisfy the conditions for
a solution.
-- Newell and Simon, ACM Turing Award Lecture, 1976
- Symbol patterns represent significant aspects of a problem domain.
- Operations on these patterns generate potential solutions to problems.
- Search is used to select a solution from among the possible solutions.
Implication: A computer that plays checkers or chess, even if it
uses a different search algorithm than we use, is displaying a form of
intelligence.
Example: Samuel's checkers program, first introduced in
1956, eventually learned to beat Samuel's himself. Samuel's program
contains an algorithm for assigning a score to the overall
state of the board after each move. The score was based on 40 or so
weighted features. The program's learning algorithm involved randomly
adjusting the weights on the features and then playing a few games
against a copy of itself with the new weights. Depending on which copy
won, the other copy would be discarded.
Comment: That doesn't seem like a very "intelligent"
learning algorithm, but it led to intelligent checkers playing.
Caveat: The PSSH is disputed by critics of AI and even by AI
researchers who use the neural network or genetic algorithm
approaches. Neural networks and GAs don't directly manipuluate
symbols. And whereas high-level thinking, such as chess playing,
logic appear to involve symbol manipulation, it doesn't seem to be
involved in low-level cognition, such as vision. However, as we will
see, both of these other approaches also require the use of knowledge
representation and search.
SOAR. Newell's work led to the creation of the SOAR project, an attempt to
develop a general cognitive architecture, based on representation and
search, that is capable of exhibiting the full range of intelligent
behavior.
- Computers are capable of implementing any effectively describable procedure.
- Everything computable is computable by
a Turing
machine.
Knowledge Representation
- Abstraction: Representing only what is necessary for a given purpose
or task.
-
Miller's 7
plus or minus 2 Law: Human short term memory is capable of storing
7 plus or minus two chunks of information at one time. (But is it more
like
3+1?
- That's why we break phone numbers into chunks: 860-297-2220.
- Expressiveness: Can the representation express all the necessary
information?
- The Roman numeral system is expressive enough to represent all positive
whole numbers: I, II, III, IV, V, VI, ...
- The Arabic number system (a positional system) is expressive enough to
represent all positive whole numbers: 1, 2, 3, ...
- Efficiency: Does the representation allow for efficient processing
of information?
- The Roman numeral system does not lead to very efficient algorithms
for multiplication and division.
- Naturalness: Does the representation provide a natural framework
for expressing the knowledge?
- Representing real numbers in binary notation is a natural way to
solve arithmetic problems on a computer.
Exercise: Calculate the product of XXVII and VIII and try to give
a general description of a roman-numeral based multiplication algorithm.
AI Knowledge Representation
Representations used in AI must be able to:
- Handle qualitative knowledge.
Example: Representing a blocks world in terms of the blocks' x,y
coordinates versus representing it in terms of the following predicates:
- clear(c).
- clear(a).
- ontable(a).
- ontable(b).
- on(c,b).
- cube(b).
- cube(a).
- pyramid(c).
- Allow representation of both specific facts and general principles
Example: The above list is made up entirely of specific facts
that describe a blocks world situation. The following PROLOG rule represents
a general principle about the blocks world:
clear(X) :- not(on(Y,X)).
In English, this says, A block X is clear, if there is no block Y that is
on X.
- Infer new knowledge from a set of facts and rules.
Example: Given the general rule about when a block is clear, we could
infer that block C is clear, since there is no block on C.
- Capture complex semantic meanings.
Example: A car cannot be described merely by listing its parts.
You must also describe its structure -- the relationships among its parts.
Example: Semantic networks have been developed to
represent of semantic meaning.
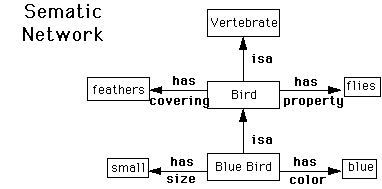
- Allow for meta-level reasoning.
Meta-level reasoning refers to reasoning about what we know,
including knowing what we don't know. For example, how do we know
not to bother searching for Donald Duck's phone number in the telephone
book? How would we get a computer to know this? Can we search for
Donald Trump's phone number in the phone book? How does common
sense reasoning figure into these questions?
Semantic Paradoxes (e.g.,
the Liar's
Paradox) Pretend the following shows both sides of a sheet of
paper:
| The sentence on the other side of this paper is false. |
| The sentence on the other side of this paper is true. |
Russell's
Paradox: In Naive Set Theory: Let R be the set of all sets that
are not members of themselves. Is R a member of itself? If so, it
contradicts its own definition? If not, then it would count as a
member of itself.
Russell's theory of types invented the notion of meta-knowledge as a
way of preventing these kinds of self-referential statement. Russell's
example (1901) showed a contradiction in naive set theory:
Problem Solving as Search
The second part of the PSSH is easily observed in human problem
solving behavior. When confronted with a problem we invariably
try to outline the possible choices and search for the best
alternative.
- Playing tic-tac-toe.
- Proving a theorem.
- Looking up a name in the phone book.
- Diagnosing a medical illness or a car problem.
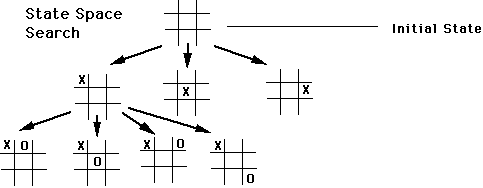 Most problems are too complex to apply exhaustive search. So we
ignore many possible alternatives because we somehow deem them to
be "irrelevant" or "unpromising." A heuristic is a rule for
deciding what states are "promising" during a search.
Most problems are too complex to apply exhaustive search. So we
ignore many possible alternatives because we somehow deem them to
be "irrelevant" or "unpromising." A heuristic is a rule for
deciding what states are "promising" during a search.
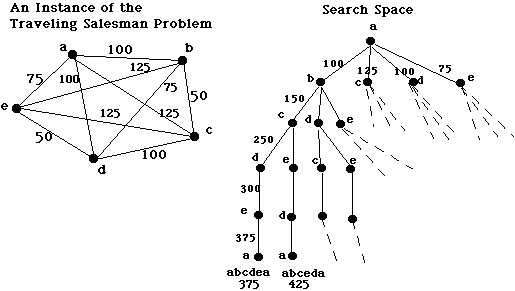
Example: In general, it takes N! operations to solve the
Traveling Salesman Problem -- that is, to find the shortest
possible path through N cities. An alternative to an exhaustive search
is the Nearest Neighbor Heuristic: At each city, choose the
nearest city as the next stop.
Homework Exercises
- In what sense is a person's name an abstraction?
- You are given two different length strings that have
the characteristic that they both take exactly one hour to
burn. However, neither string burns at a constant rate. Some sections
of the strings burn very fast, other sections burn very slow. All you
have to work with is a box of matches and the two strings. Describe an
algorithm that uses the strings and the matches to calculate when
exactly 45 minutes has elapsed.
- Here's a Lewis Carroll favorite: A farmer needs to
cross a river with his fox, goose, and a bag of corn. There's a
rowboat that will hold the farmer and one other passenger. The problem
is that the fox will eat the goose, if they are left alone, and the
goose will eat the corn, if they are left alone. Develop a
knowledge representation scheme and draw a portion of the
search space.
- Have you heard this one? A farmer lent the mechanic
next door a 40-pound weight. Unfortunately the mechanic dropped the
weight and it broke into four pieces. The good news is that according
to the mechanic, it is still possible to use the four pieces to weigh
any quantity between one and 40 pounds on a balance scale. How much
did each of the four pieces weigh? ( Hint: You can weigh a 4-pound
object on a balance by putting a 5-pound weight on one side and a
1-pound weight on the other.)
- Show that the nearest neighbor heuristic is not optimal -- that
is, it doesn't necessarily lead to the shortest possible path -- for a
5-city instance of the traveling salesman problem.




